
This was the selected method because there was more pixel redistribution due to the high level of the original distortion. For the sake of increased accuracy I used 2 extra GCP's, using a total of 12 to correct the distortion.ĭue to the high level of correction being done, the resampling method I used was the Bilinear Method. This required that we place a minimum of 10 GCP's on both the reference and distorted image. Due to the high level of distortion, the operation used was a 3rd order polynomial spatial interpolation. This can easily bee seen by simply overlaying the two images, and using the swipe tool to see how the features are off from there actual location. There is one image that is geometrically accurate and one that is not. This part of the lab covered a part of Sierra Leone, Africa, and required that I do similar steps as I used above, but this time the components are both images. One should always strive to have the lowest values possible for RMS error in order to ensure an accurate image.
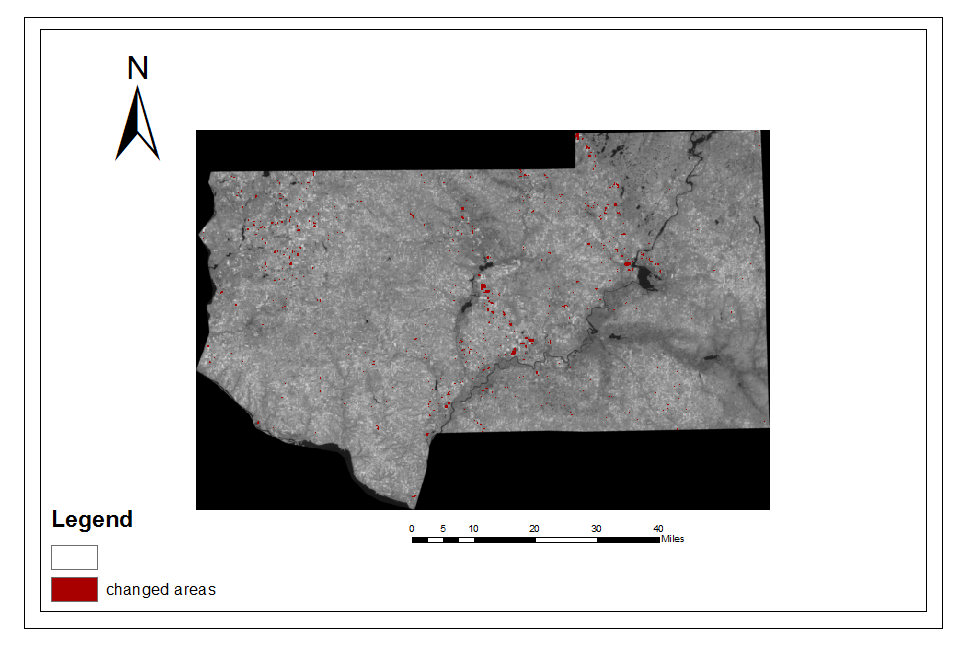
I was able to reach RMS error values lower than the requested 2 % for all four of my GCS points. Since the adjustment being made are relatively minor, it is appropriate to just use a nearest neighbor resampling method. With that being said, its advised by the lab to use 4 for the sake of maximized accuracy. The computer than uses these GCP's in algorithms that adjust the image to the points on the map, creating an image that is now has accurate geographic properties, closer to their real world location. The number GCP's needed for a given operation depends on the degree of the polynomial operation being done. Since the adjustment is only a minor first order polynomial (linear adjustment) its only necessary to use 3. to do this students placed ground control points (GCP's) on the same locations on the image (distorted Image) and the map (reference source). Students conducted a first order polynomial special interpolation technique. In this case, the image and map in use were covering Chicago and surrounding areas near the Wisconsin and Illinois border. In the first part of the lab, students worked with image-to-map rectification operations. we used multiple scale images and also a digital elevation model to create the output image where relief displacement and other geometric errors have been removed, along with an overall improvement of accuracy.įor all activiaties done in this lab, the images used were from The United States Geological Survey 7.5 minute digital raster graphic data collection. By using the Lecia Photogrammetric Suite (LPS) digital photogrammetry tool, students used control points and tie points to triangulate, and ultimately orthorectify the images we collected into one. The subject area of the images being corrected was that of Palm Springs, California. Orthorectification is a very intensive process that involves heavy input from the user. Here we see a smoke tower that is altered due to relief displacement The result is taller features displaying relief displacement, where they are oriented at odd angles in relevance to their actual appearance in the real world This error is produced when an image has height variation, but has the same general scale. The image produced was accurate in its relief, but also introduced an element of geometric scaling error. R= radial distance object is from principle point H'= height of image taken - height of area above/below sea level.Ĭalculating relief displacement was done using the equation: D = (hxr)/H where The calculating of scales was done using the equation: s = f/H' where The measurement of area/perimeters was done via the ERDAS imagine digitizing tool. In the first 3 sections of the lab, students conducted used both mathematical and computer generated methods to discover either the scales, record area/perimeters, and measure relief displacement. Moreover this lab also offers an introduction of to stereoscopy and satellite image orthorectification.
Specifically, this lab is tailored to train students to better understand the mathematics involved in calculating scales, measuring areas and perimeters of features, and calculating relief displacement. The goal of this laboratory exercise was to develop the skills necessary to preform photogrammetric tasks on aerial photographs or satellite images.


 0 kommentar(er)
0 kommentar(er)
